▼▼▼← 学習機械について（１）：Cellular Automata
▼▼▼← 学習機械について（２）：Fuzzy Automata
大学院論文輪講（Ｍ１）
｛後・評 08.3｝IEEE Computer の2008年1月号の論文：
An Assessment of Integrated Digital Cellular Automata Architectures、
によると、
４０年近く前に読んだノイマンのセルラーオートマトンが注目されているらしい。
当時の私の輪講資料（1969）では「現在あるような素子で実現した場合には、経済的問題があり、またコンピュータとしても幼稚なものになるので、この分野が工学として確定するためには、新しい素子を必要とするようである」と記載しているが、この「新しい素子」の時代がきたらしい。
追伸１：
1994年からセルラーオートマトンに関する
国際会議 ACRI
が開催され、今年で８回目らしい。
追伸２：
1996年に多細胞動物で”不老不死”のクラゲ（
ベニクラゲ）発見の論文発表があったらしい．
最近のテレビ番組で自己再生シーンを見たが，これは，この資料の「今後の展望と学習機能」 で
「自己増殖について・・・、あらかじめのプログラムにしたがって、正確なコピーを作る能力であって、・・・、全体が破壊していく前にコピーを作って、死を免れるようなこと・・・、システムの永久性がある。」に相当するのでは！？
｛後・評｝最後の今後の展望で、「状態の遷移関数に確率を導入して、ある程度の不確かさを与えると、自己増殖の過程で、多くの不良品（退化）に混じって、進化した子孫が生まれる可能性がある。」と述べたが、これは、後に出て来る遺伝的アルゴリズムの先取りだった？！
｛後・評｝情報処理学会誌（2003年4月号）20世紀の名著名論で、
和田英一先生が「E. F. Codd: Cellular Automata」を取り上げておられる。
この本の海賊版（1970頃の違法文化）所有。
当時の私の評価は「倹約の過ぎたCodd」（下記のp.17参照）。
###########################################################
（注）下記は手書きテキストの音声入力による電子化
→★★★原本PDF
大学院論文輪講資料 １９６９年１１月２８日
学習機械について（１）：Cellular Automataの場合
斎藤研 М１ 中所武司
目次
１．セルラーオートマトンの歴史
２．２９stateのモデル
2.1 状態及び遷移法則
2.2 ノイマンの機械
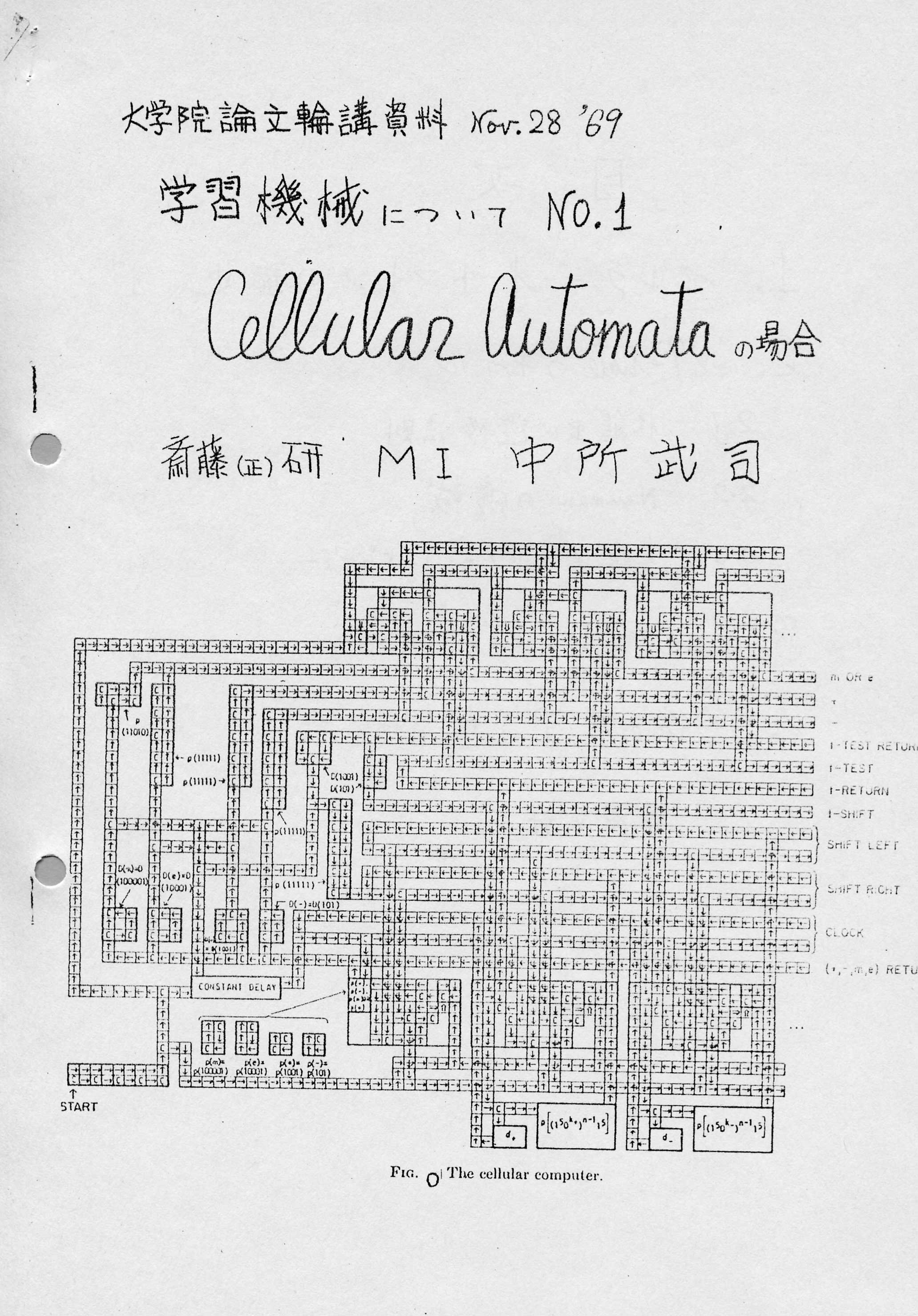
2.3 Ｌｅｅのセルラーコンピュータ
３．Ｃｏｄｄの８stateのモデル、
４．今後の展望と学習機能、
参考文献
１．セルラーオートマトンの歴史
フォンノイマンは、１９４０年代後半にオートマトン理論を展開し始め、特に人間の神経系あるいは巨大なコンピュータに興味を持ち、自己増殖の問題を提出した。彼は自己増殖のモデルとして、動的モデル、セルラーモデル、ニューロンを一つの有限オートマトンと考えた励起閾値疲労モデル、ニューロンの興奮、閾値作用、不応期の特性を支配する偏微分方程式に基礎をおく連続モデルなどを考えたが、１９５２年から１９５３年にかけて、このうちのセルラーモデルを発展させることにより、彼自身のオートマトン理論における主要問題である万能性、構成可能性、自己増殖、進化などについて、ある程度解決できた。
彼の考えたセルラーオートマトンは次のようなものである。正方形のセルで無限に満たされたセルラー平面を構成する各セルは、全て同じ有限オートマトンで、その状態数は２９．そのneighborhoodの数は上下左右の４個と、自分自身、そして、時刻t+1のセルの状態は、時刻tにおける５個のneighborhoodの状態と遷移法則によって決まる。そして、この有限オートマトンは、静止状態Ｕを持ち、この無限のセルラー平面は、常に、有限個のセルを除いて、全てこのＵの状態にある、というものである。しかし、ノイマンは、１９５７年に、この２９stateのモデルを複雑化させる前に、弱冠５３歳で世を去った。
その後、この理論の展開は、あまり急速には起らなかったが、１９６６年にA.W.Burksがノイマンの遺稿を編集して製本化したことから、だんだんこの分野に興味を持つ人々が多くなってきた。
Ｃ．Ｙ．Ｌｅｅは、ノイマンの２９stateのモデルを受け継いで、第１には、初歩的なコンピュータの構成を試み、第２には、論理設計の新しい方法を示そうと試みた。彼の見解では、現在あるような素子で実現した場合には、経済的問題があり、またコンピュータとしても幼稚なものになるので、この分野が工学として確定するためには、新しい素子を必要とするようである。
一方、Ｅ．Ｆ．Ｃｏｄｄは、ノイマンの２９stateのモデルを出発点として、それを発展させていくような方法をとらないで、Ｊ．Ｗ．Thatcherが新たに作成した定義や形式を利用して、ノイマンのモデルより、もっと簡単なもの研究した。neighborhoodの数はノイマンと同じ５個にして、２stateのものから始めた。そして、neighborhoodの数を増加するより、stateの数を増加する方が良好な結果が得られることが分かり、結局８state、５neighborhoodのセルラーオートマトンは、ノイマンの２９state、５neighborhoodと同じ計算及び構成の操作ができるうえに、それ以外の能力も備えることが分かった。
また、ノイマンの２９stateのモデルでは、状態の変化は時間によらなかったが、Ｊ．Ｈ．Hollandは、時間によっても状態が変化するものを考えた。
＜以下、４節まで、省略＞
２．２９stateのモデル
2.1 状態及び遷移法則
2.2 ノイマンの機械
2.3 Ｌｅｅのセルラーコンピュータ
３．Ｃｏｄｄの８stateのモデル、
４．今後の展望と学習機能
ノイマン、Ｌｅｅ、Ｃｏｄｄのモデルは、先に見たごとく、互いに相当異なっており、３者３様で、堅実一辺倒のノイマン、技巧に溺れたＬｅｅ、倹約の過ぎたＣｏｄｄと言えそうである。しかし、機能的な面から見ると、どれも大差なく、（万能チューリングマシン＋自己増殖）の能力を持つ。
そこで、計算機として見た場合、Ｌｅｅの指摘するように、今のディジコンに比べ、幼稚なものになってしまうので、今後も計算機を目的とした場合の将来性は、あまりないが、このようなモデルの１属性として、計算能力が問われる場合は生きてくると思われる。すなわち、例えば、計算能力として四則演算だけのできる人間と計算機では、その価値は異なる。計算機にとっては、四則演算能力は自己の存在そのものであるが、人間にとっては、一つの属性でしかない。したがって、人間社会では、前者は、より高度の計算機によって、その存在価値を失うが、後者は、それにもかかわらず、四則演算能力は、その存在価値を高めるのである。
ではつぎに、自己増殖についてはどうであろうか。
これは、あらかじめのプログラムにしたがって、正確なコピーを作る能力であって、そこに進化が見られないという限界性があるけれども、例えば、あるシステムの１機能を受け持つ部分が破損したとき、それによって全体が破壊していく前にコピーを作って、死を免れるようなこと、あるいは、手遅れの場合でも、自分の子供を作ってから死ぬというようなことができるので、システムの永久性がある。それは封建時代の身分制度による体制維持に似ていて面白い。
しかし、このモデルは進化しない、あるいは学習機能を持たないため、厳しい自然の中で生き抜くには、あまりに致命的な欠陥と言える。そこで、このモデルの学習機能の可能性を見てみよう。
「学習」ということが明確になっていない段階で、学習機能を云々するのは初めから無理があるが、もし、生物における学習がニューロンによるものだとすれば、このニューロンの機能は、現在わかっている限りでは、この有限オートマトンセルでモデル化できるので、このモデルが、将来、学習を行うようになる可能性はあると思う。また、状態の遷移関数に確率を導入して、ある程度の不確かさを与えると、自己増殖の過程で、多くの不良品（退化）に混じって、進化した子孫が生まれる可能性がある。しかし、現段階では、そのメカニズムにまで立ち入って、学習機能を云々することは避けたい。
参考文献
1. Von Neumann, J., “The Theory of Self-Reproducing Automata” ed. A.W.Burks, Univ. of Illinois Press, Urbana, Illinois. 1966.
2. Lee, C.Y., “Synthesis of a Cellular Computer” in “Applied Automata Theory” ed. J.T.Tou, Academic Press, 1968.
3. Codd, E.F.,”Cellular Automata” Academic Press, 1968.
p.i
（中略）
p.17
p.18
大学院論文輪講（Ｍ２）
（注）関連ブログ 2024.1
→「ファジイ理論」を読んで
（注）下記は手書きテキストの音声入力による電子化
→★★★原本PDF
大学院論文輪講資料 １９７０年６月２６日
学習機械について（２）：Fuzzy Automataの場合
斎藤研 М２ 中所武司
目次
１．はじめに
２．fuzzy集合
３．fuzzyアルゴリズム
４．fuzzy集合の応用
4.1 fuzzyオートマトン
4.2 学習システムへの応用
4.3 パターン識別への応用
５．おわりに
参考文献
１．はじめに
我々の世界にある物や状態は、それがあるクラスに属するか否かを判定する基準が明確には定まっていない場合がしばしばある。例えば「美人」、「右翼」，「大きな数」などがそれである。これらは明らかに通常の数学的意味における集合を構成していない。しかしながら、そのように不正確に定義された概念は、人間の思考に関するもの、とりわけ、人工知能、パターン認識、情報処理などに重要な役割を果たしている[2]。
そこで、カリフォルニア大学のSadehは、１９６５年にmembership関数なるものを導入して、定義のあいまいな概念を量的に特徴づけるfuzzy集合を提案し、議論を展開した[1]。
その後、この考えは、多方面で応用されつつあるが、本輪講では、特に、Wee and Fuの論文[3]を中心に、fuzzy集合の、学習系への応用について考えてみたい。
＜以下、 ５節まで、省略＞
５．おわりに
fuzzy集合は、そのmembership関数を０と１に限れば普通の集合になることからわかるように、集合概念の一般化であり、したがって、fuzzyオートマトンは、普通の決定オートマトンや確率オートマトンの一般化である。４。そのため、議論展開が、従来のものと似ることは避けられないが、ここで述べたWee and Fuのパターン認識の応用は、その本質が、fuzzyオートマトンよりも、むしろ、従来の統計的手法にあるとも考えられ、まだ十分にfuzzy集合の概念を生かした応用とはいえない。その点で、既成の意味の拡張ということにとらわれず、fuzzy集合の概念だけを原点とした独自の展開が望まれる。
いずれにせよ、このようなfuzzy問題を扱うとき、その扱い方がfuzzyにならないように気をつけなければならない。
参考文献
1. L.A.Sadeh, ”Fuzzy sets,” Information and Control, vol.8, pp.338-353, June 1965.
2. L.A.Sadeh, ”Fuzzy algorithms,” Information and Control, vol.12, pp.94-102, 1968.
3. W.G.Wee and K.S.Fu, “A formulation of fuzzy automata and its application as a model of learning systems,” IEEE, vol.SSC-5, No.3, July 1969.
p.i
（中略）
p.12
