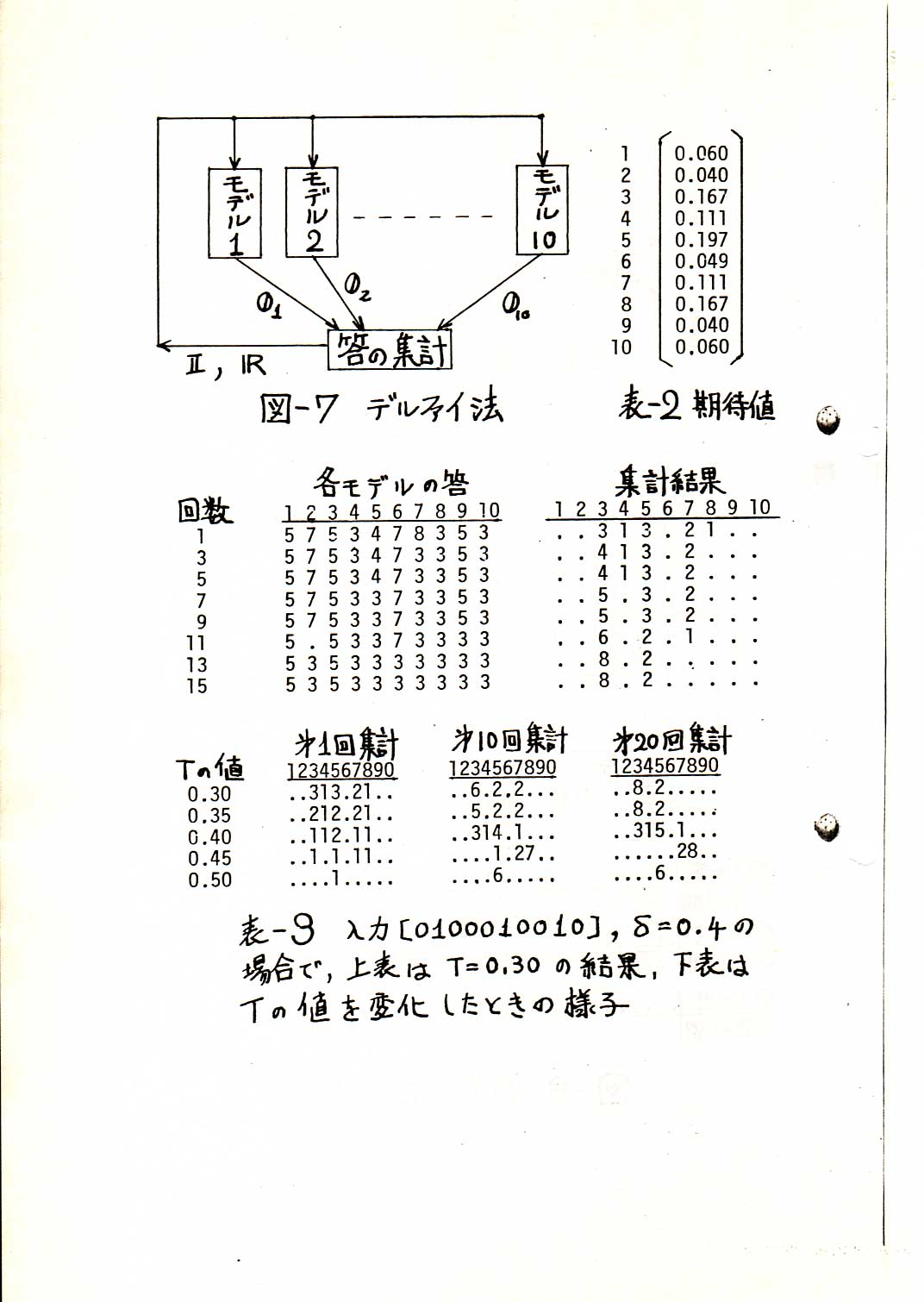
p.10
p.11
p.12
p.13
ɽ��

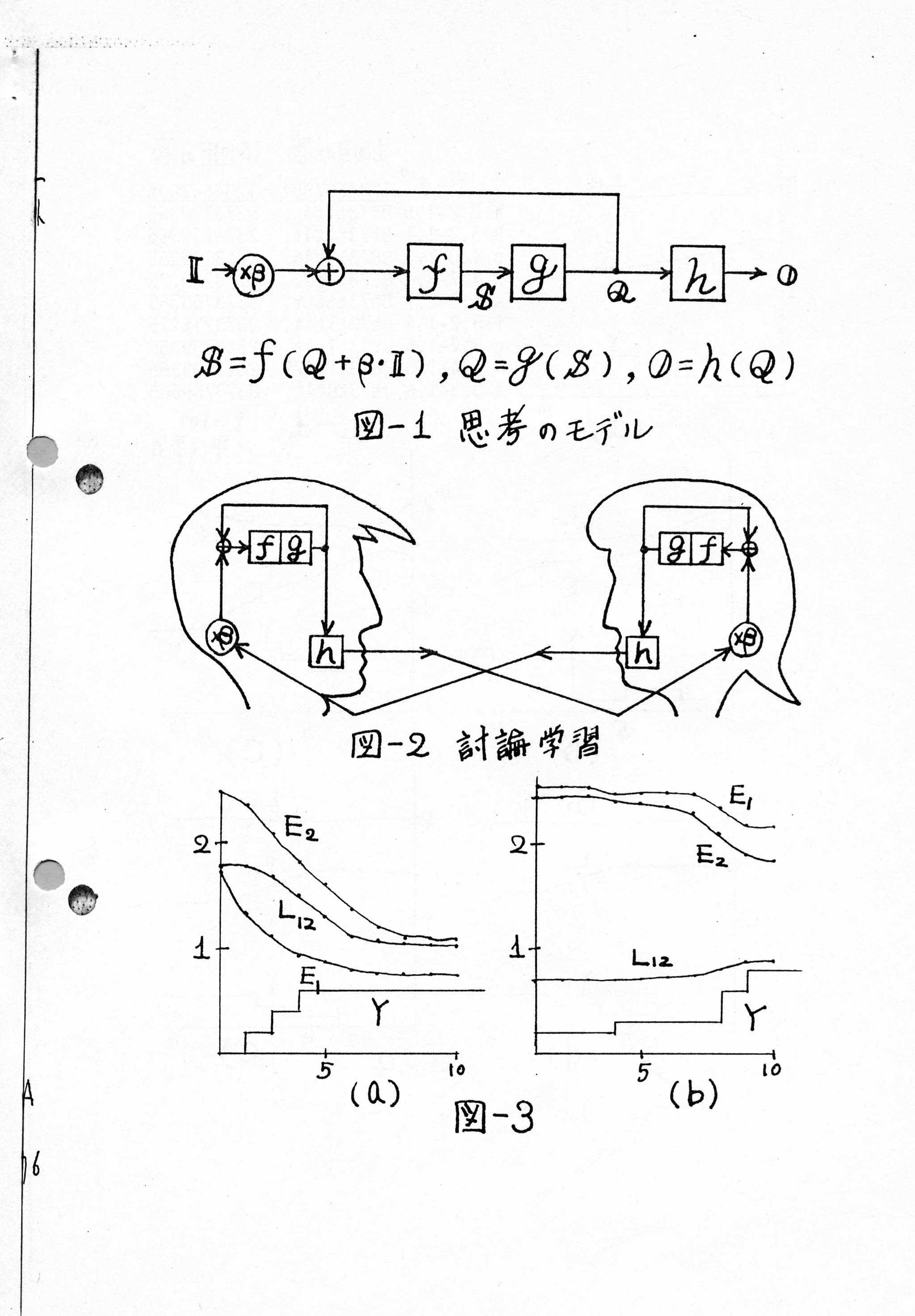
p.1

������
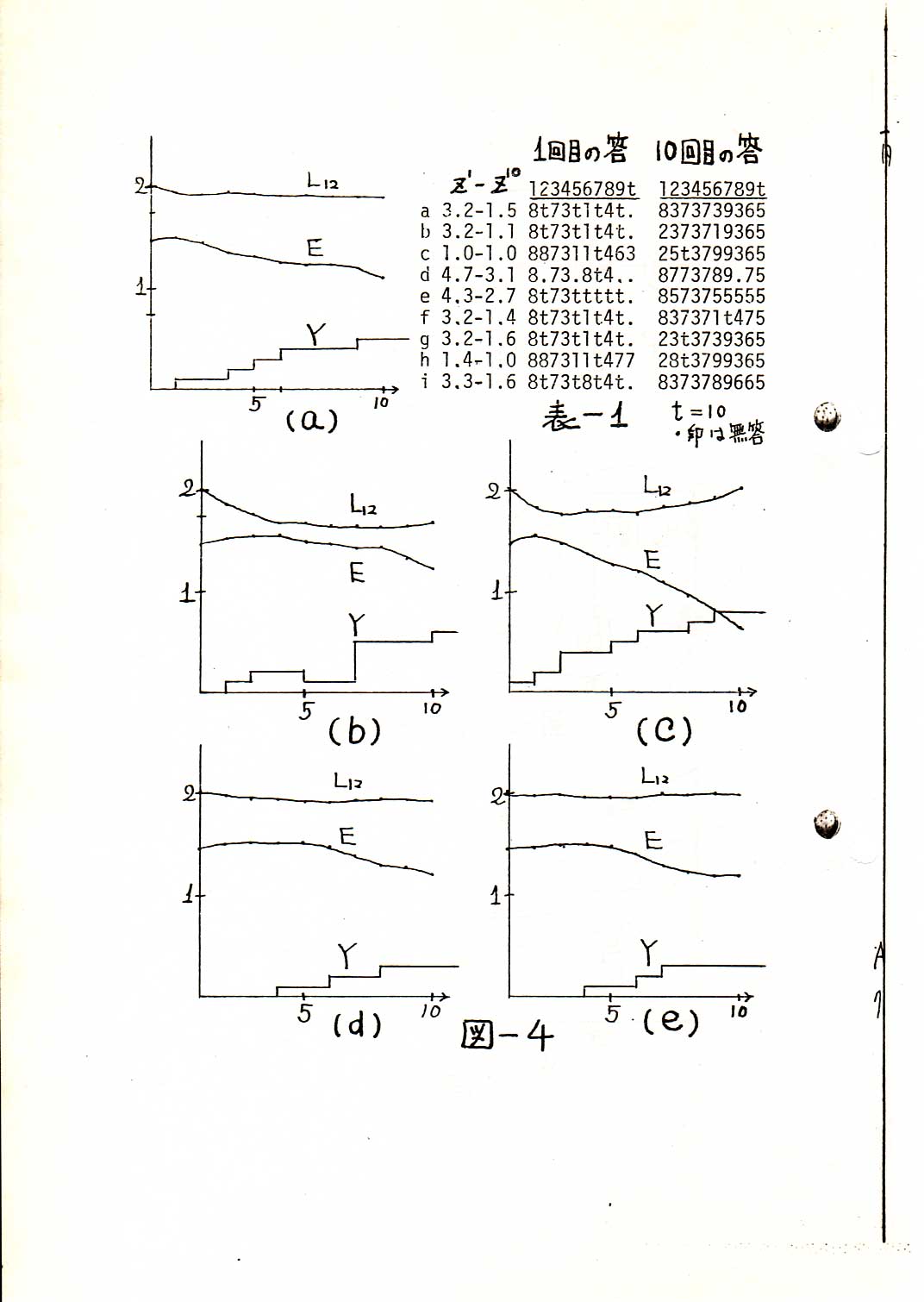
p.8

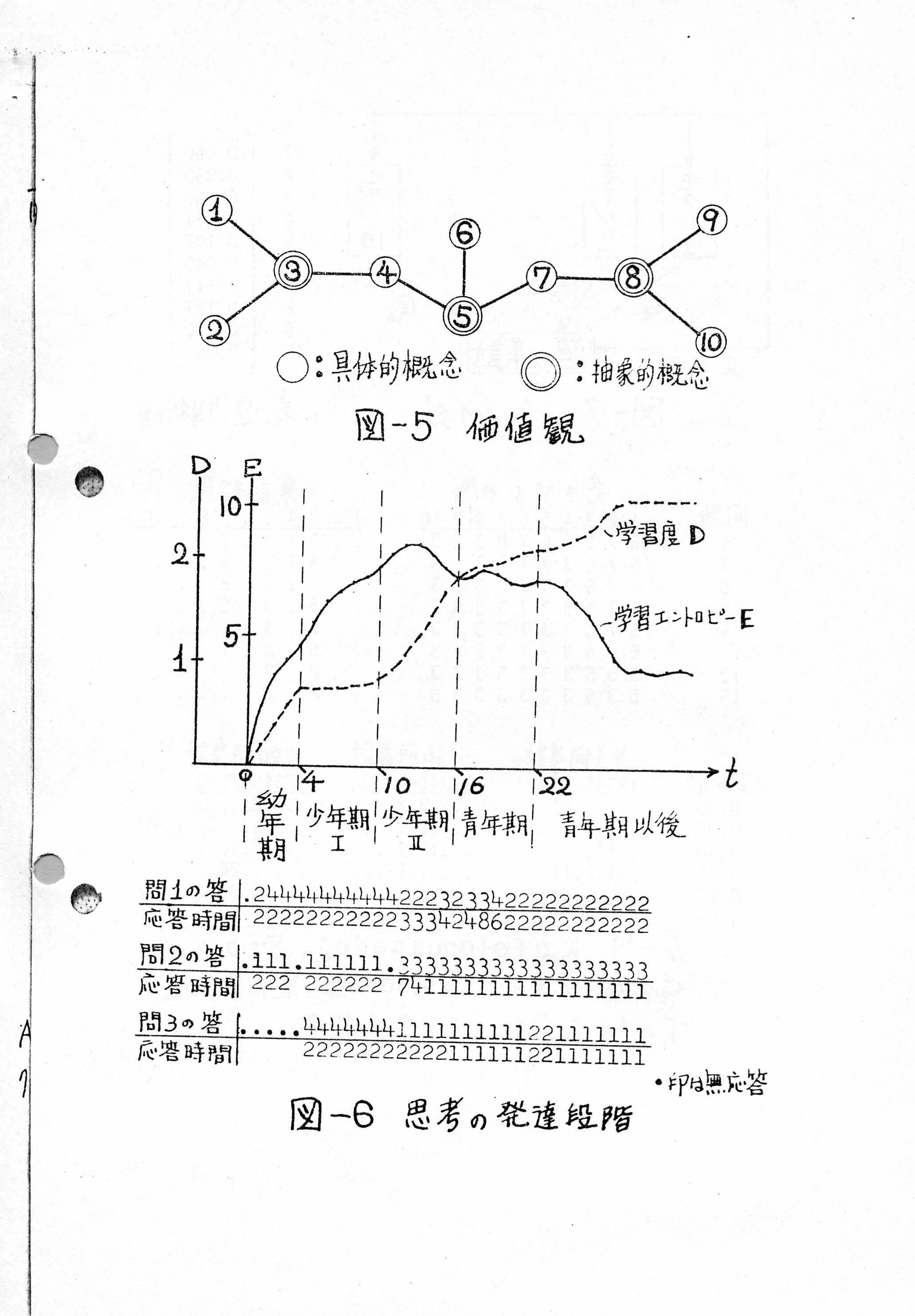
�Ͳ����Υ��ߥ�졼�����
����Ƥ���ؽ�¾����������ˤĤ��ơ��� Simulation of Thinking Process - In case of Learning by Discussion, etc. - �����ʡ���ƣ���ˡ������ء��������� Takeshi Chusho and Masao Saito ��������ǯ���������






